The value of the solar radius at the reference distance of 1au is one of the fundamental quantities needed to perform very precise eclipse computations and is the the most uncertain parameter up to now compared to ephemerides for the position of the centres of mass of the Sun and Moon, models for the orientation of the Earth and Moon and topography of the Moon and Earth.
The standard value of the solar radius has been determined by Auwers in the late 1800’s and has remained unchanged for more than a century: 959.63”, and it is still used in all published eclipse predictions and softwares. We note that Solar Eclipse Maestro, a commonly used eclipse software, albeit it defaults to using the standard radius, it allows the user to modified its value.
Specific domains of solar physics and astronomy may use other, more suitable, values of the solar radius for example, in the context of conversion factors, the IAU had recommended a nominal value for the solar radius equivalent to 959:23″, based on helioseismic measurements.
We are interested in the value of the eclipse solar radius, the radius to be used in very precise computations that predict the internal contact times of solar eclipses to a high level of accuracy. In particular, a radius that best reproduces the visual experience of a total solar eclipse. Such a solar radius corresponds closely with the notion of complete photospheric extinction where totality is defined as the period of time during which the photosphere is fully and unequivocally blocked by the limb of the Moon.
Auwers’ value is often quoted with two decimals. This has unfortunately fostered a false sense of accuracy. In reality the eclipse solar radius can be quite comfortably estimated to within 0.1″ (but certainly not to within 0.01″, reliably and reproducibly).
So, how accurately should contact times for a total solar eclipse be forecasted by computation? Let’s say at the level of a tenth of a second for eclipses occurring close to the current epoch. But what is the impact of using different values for the solar radius?
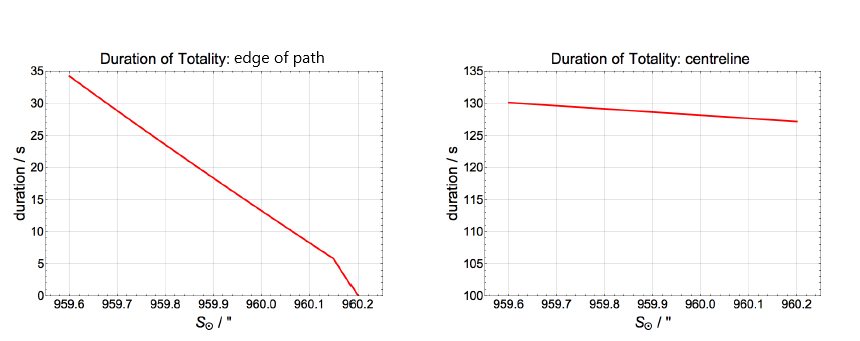
If we assume that the most suitable (eclipse) solar radius to be used in eclipse computations is around 960″, we can look at how much the duration of totality changes by using this value instead of the standard radius (equivalent to 959.63″). Let’s take the example of the TSE2017 and a location near the border between Oregon and Idaho, as shown in this figure:
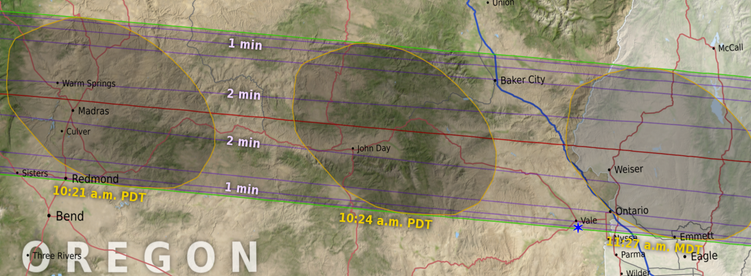
On a location on the centreline, the duration of totality drops from 130s to 128s. For a location very near the southern edge of the eclipse path, the duration of totality goes from 34s to 13s. The impact of substituting the standard solar radius with a more appropriate one has a noticeable impact, an impact that becomes more and more pronounced the further away from the centreline.
